Beispiele:
- Auflade- und Entladekurve einer Kombination aus Kondensator und Widerstand
- Abnahme von radioaktiver Strahlung
- Aufheizen, Abkühlen eines Kühlkörpers
- Bakterienwachstum
Oftmals reichen wenige Messwerte aus, um die Funktion mathematisch bestimmen zu können. Das hat den Vorteil, dass man z.B. bei Vorgängen mit sehr langer Zeit gar nicht so lange warten und messen muss um den vollen Kurvenverlauf zu sehen, wie es des Anschein hätte. Es ist oftmals auch günstig die Funktion als Zahlenwerte genau zu kennen, da sich damit auch z.B. in Regelungen oder mit digitaler Hardware leicht rechnen läßt.
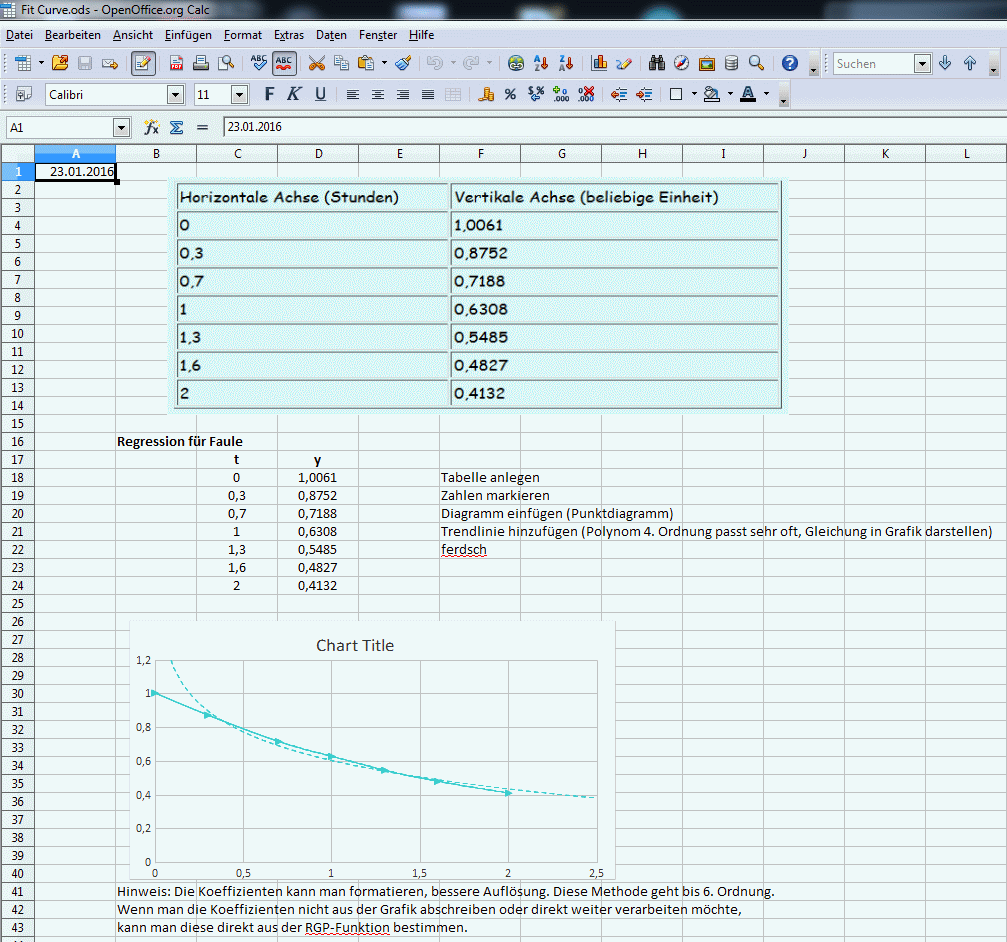
Messwerte als Beispiel:
| Horizontale Achse (Stunden) | Vertikale Achse (beliebige Einheit) |
| 0 | 1,0061 |
| 0,3 | 0,8752 |
| 0,7 | 0,7188 |
| 1 | 0,6308 |
| 1,3 | 0,5485 |
| 1,6 | 0,4827 |
| 2 | 0,4132 |
Dieses Beispiel könnten Messwerte sein, die eine Person etwa alle halbe Stunde von einem Messgerät abgelesen und notiert hat. Die Person erwartet, dass sein Vorgang von der Größe 1 nach einer unbekannten Zeit auf die Größe von 0 absinken wird. Nehmen wir an, die Person muss an der Anlage anwesend sein genau zu dem Punkt y=0,1 aber wann genau ist das?
Er hat bereits seit 2 Stunden gemessen, daneben gesessen und die Größe beträgt immer noch etwa y=0,4 wann endlich ist es y=0,1 ? Er kann leider nicht so lange neben der Anlage sitzen bleiben um das Messgerät zu beobachten. Die Person versucht auszurechnen, wann ein günstiger Zeitpunkt t=? ist um wiederzukommen um den gesuchten Punkt y=0,1 abzuwarten.
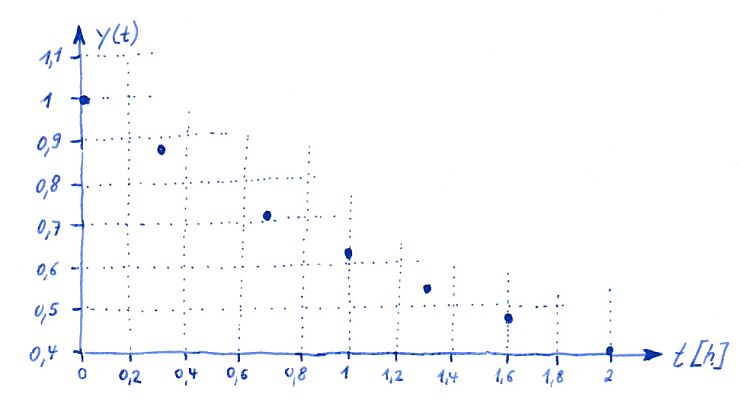
Exponentielle Grundgleichung:
y(t) = A * e ^ (B*t)diese Grundgleichung ist vermutlich passend zu den gemessenen Werten. Diese Annahme muss physikalisch richtig sein, für einen korrekten Fit. Der ganze Fit ist nur so viel wert, wie der physikalische Vorgang auch der Grundgleichung gehorcht, diesen Satz gilt es zu verinnerlichen.
- Das entscheidende ist der Fit geschieht nicht direkt mit der Exponential Funktion, sondern der Fit erfolgt mit einer Geradengleichung, die mittels einer logarithmischen Funktion dahin umgewandelt wurde. Hierzu bedienen wir uns dem Hilfsmittel einer Transformation der Gleichung zunächst in den logarithmischen Bereich.
- y(t)=A*e^(B*t) läßt sich auch schreiben als: ln[y(t)]=ln[A*e^(B*t)] ---------- beide Seiten der Gleichung sind nun transformiert in den logarithmischen Bereich. Es ist zulässig beide Seiten zu logarithmieren, da in der Mitte immer noch stets das Gleichheitszeichen steht. Das ist das gleiche, wie wenn man aus 2=2 dann 2*c=2*c oder ln(2)=ln(2) schreiben würde. Solange man mit beiden Seiten des Gleichheitszeichnen dasselbe macht, hat man hierfür die Freiheit.
- Wir wandeln nun die Logarithmen Gleichung in eine Geradengleichung, da für die Geradengleichung ein ganz einfaches Verfahren existiert, um daraus einen Fit zu bilden.
- Wir ersetzen z=ln(y)
- Wir ersetzen a0=ln(A)
- Wir ersetzen a1=B
- Aus dieser Substitution entsteht die notwendige Geradengleichung.
- z(t)=a0+a1*t ist eine Geradengleichung.
- nochmal: aus y(t)=A*e^(B*t) ==> ln[y(t)]=ln[A*e^(B*t)] ==> z(t)=a0+a1*t
- z(t)=a0+a1*t läßt sich nach der Methode der kleinsten Fehlerquadrate leicht zu einem Fit verarbeiten.
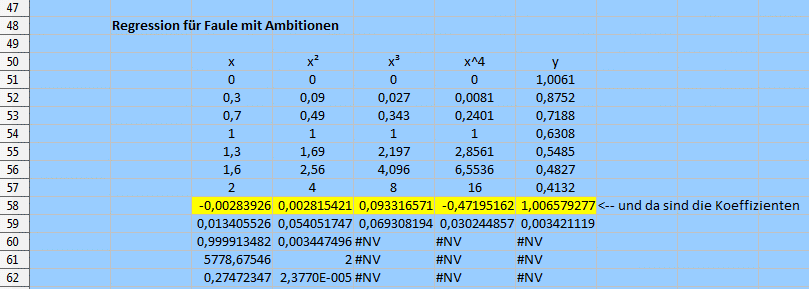
Formel zur Berechung der Koeffizienten der Geradengleichung:

Summen für die obigen Gleichungen:
| t= | z= z=ln(y) | t*z= | t*t= |
| 0 | 0,0060994 | 0 | 0 |
| 0,3 | -0,1333 | -0,04 | 0,09 |
| 0,7 | -0,3301 | -0,2311 | 0,49 |
| 1 | -0,4608 | -0,4608 | 1 |
| 1,3 | -0,6006 | -0,7807 | 1,69 |
| 1,6 | -0,7283 | -1,1653 | 2,56 |
| 2 | -0,8837 | -1,7674 | 4 |
| Summe=6,9 | Summe=-3,1307 | Summe=-4,4453 | Summe=9,83 |
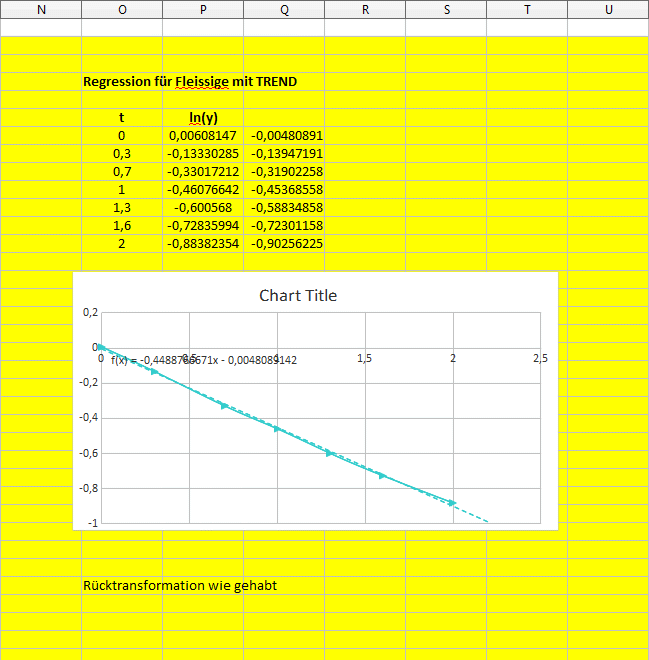
Linear Fit Geradengleichung:
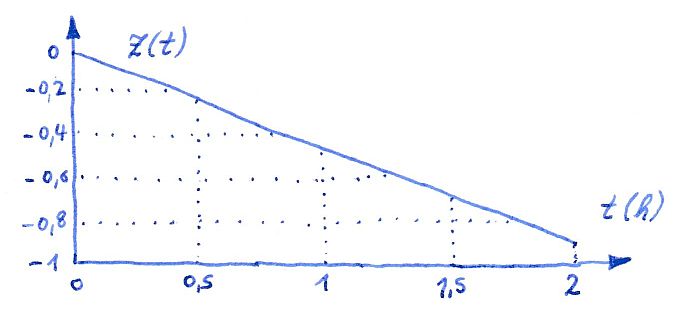
Das hier sind immer noch die Messergebnisse unserer Person !
Allerdings nicht als expobentielle Funktion sondern transformiert als logarithmische Funktion.
Rücktransformation der Geradengleichung zur exponentiellen Funktion:
A = e ^a0A=0,9952
B=a1
B=-0,4488
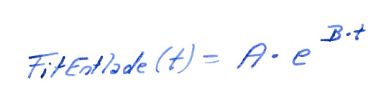
FitEntlade(t)=0,9952*e^-0,4488*t
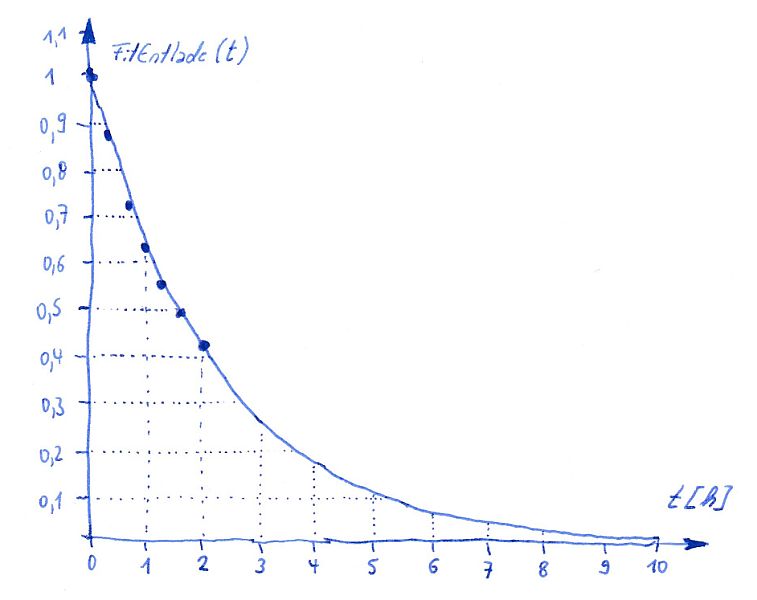
Mit dieser exponentiellen Funktion lässt
sich das Messobjekt nun zu jedem Zeitpunkt bestimmen. Wir erinnern
uns, die Person wollte wissen wann sein Messwert auf y=0,1 abgesunken
ist, hier aus dem Diagramm abgelesen zum Zeitpunkt t=5,1 Stunden.
FitEntlade(5,1h)=0.1008933
Durch Ausprobieren und Annähern der
passenden Werte oder durch bilden der Umkehrfunktion läßt sich der
genaue Wert bestimmen. Die Person weiß nun präzise zu welchem
Zeitpunkt genau sie zum Beobachten des Messwert y=0,1 am Messobjekt
sein sollte.
Berechnung der Zeitkonstante Tau:
Aus der exponentiellen Funktion ist es
leicht die Zeitkonstante des System zu berechnen.
Diese ist definiert zu 36,8% des Endwert der Entladekurve (exponentieller Abfall).
Diese ist definiert zu 63,2% des Endwert der Ladekurve (exponentieller Anstieg).

FitEntlade(2,228h)=0,9952*e^(-0,4488*2,228h)
FitEntlade(2,228h)=0.3661
korrekt, das entspricht 36,8%

FitLade(t)=0,9952*[1-e^(-0,4488*t)]
Diese ist definiert zu 36,8% des Endwert der Entladekurve (exponentieller Abfall).
Diese ist definiert zu 63,2% des Endwert der Ladekurve (exponentieller Anstieg).

FitEntlade(2,228h)=0,9952*e^(-0,4488*2,228h)
FitEntlade(2,228h)=0.3661
korrekt, das entspricht 36,8%
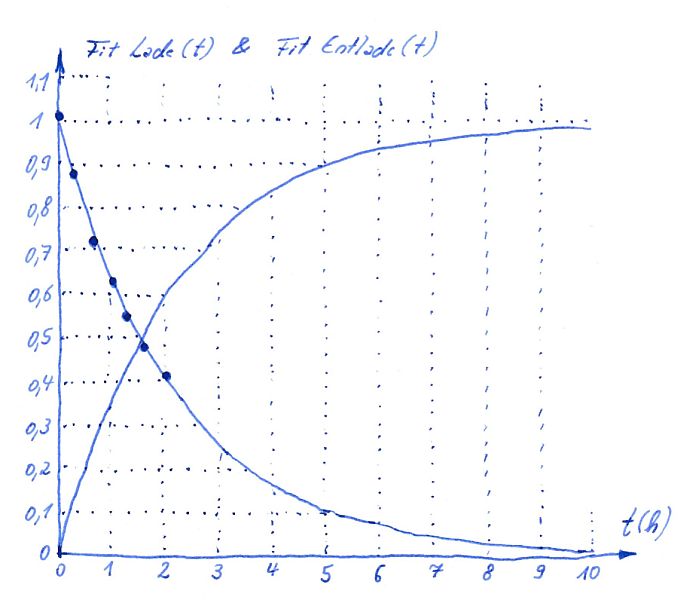
Exponential Funktion einer zugehörigen Ladekurve:

FitLade(t)=0,9952*[1-e^(-0,4488*t)]
Interessiert man sich für die zugehörige
expoentielle Ladefunktion, so kann diese aus den bisherigen
Ergebnisse gebildet werden. Beide nutzen die gleichen Koeffizienten a0
und a1.
Exponentielle Lade- und Entladefunktion in einem Diagramm:

Der Bericht wurde erstellt als eigene
Merkhilfe für Dinge, die man einmal tun musste - und man sich aber
sicher ist, dass man das ganze Verfahren nach einem halben Jahr schon
wieder vergessen hat, mit der Folge sich zuerst wieder durch
Mathematik Bücher durcharbeiten zu müssen. Die eigenen Dinge wieder
einzulesen gelingen meist effektiver.
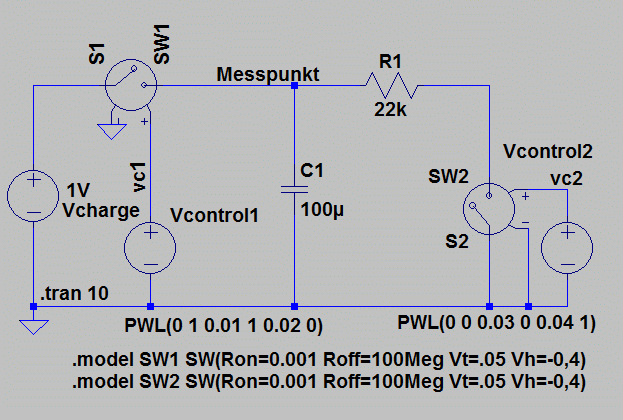
LTSpice Simulation einer exponentiellen Entladung
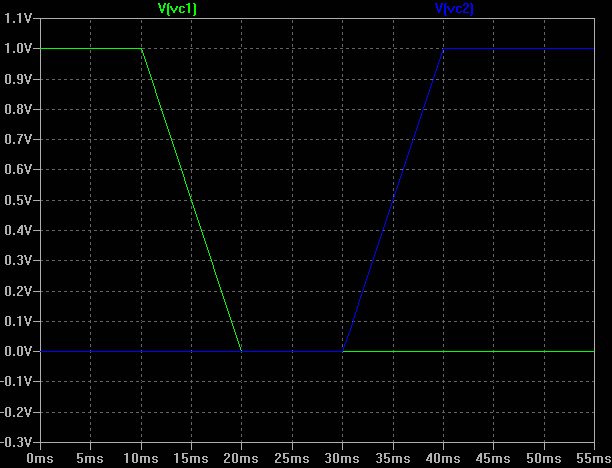
Zeitlicher Verlauf der Ansteuerung
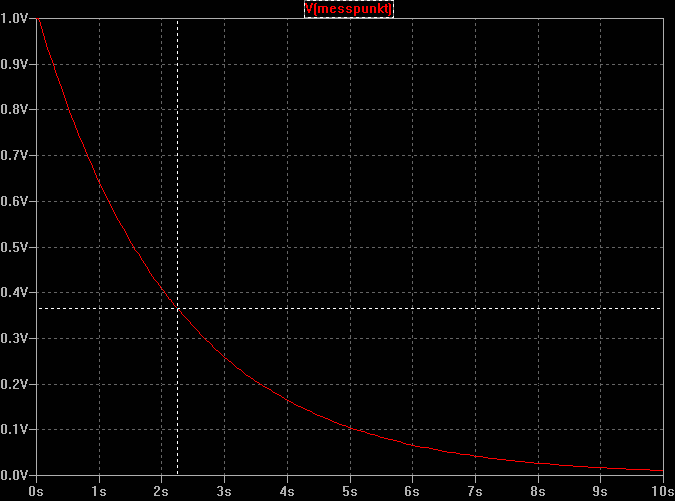
Beispiel einer exponentiellen Lade- und Entladefunktion an einer RC Simulation:

LTSpice Simulation einer exponentiellen Entladung

Zeitlicher Verlauf der Ansteuerung
t=0 der Kondensator C1 wird über den
Schalter S1 aufgeladen auf 1 Volt
t=10ms, C1 ist bereits aufgeladen und wird von der Quelle Vcharge getrennt
t=20ms bis t=30ms, C1 ist nur hochohmig belastet
t=30ms, Schalter S1 beginnt zu schließen
t=35ms, Kondensator C1 100µF wird über S2 und R1 mit 22kOhm entladen.
t=10ms, C1 ist bereits aufgeladen und wird von der Quelle Vcharge getrennt
t=20ms bis t=30ms, C1 ist nur hochohmig belastet
t=30ms, Schalter S1 beginnt zu schließen
t=35ms, Kondensator C1 100µF wird über S2 und R1 mit 22kOhm entladen.


Diese RC Kombination aus R1=22k und
C1=100µF hat eine Zeitkonstante Tau=2,2Sekunden.
Tau=100µF*22k
Tau=100*10^-6 *(As/V) * 22000*(V/A) ==> die Einheiten lassen sich kürzen auf s = Sekunde
Tau=2,2 Sekunden
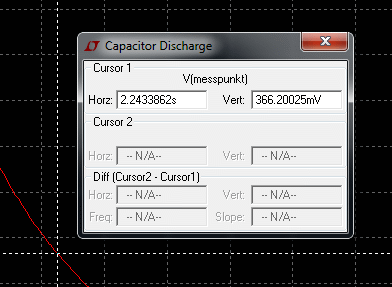
In der Cursorposition bei ca. 2,2s ist die Kondensator Spannung auf ca. 36,8% abgesunken, was dem Wertepaar für Tau entspricht.
Man vernachlässige bitte die wenigen Millisekunden Verzögerung in der Simulation durch das Aufladen von C1. Diese Simulation ist zugleich ein schönes Beispiel hierfür, wie man in LTSpice die Schalter editieren muss, auch zum späteren Nachschlagen geeignet, denn ich vergesse auch ständig immer wieder die Syntax zum Einstellen der Schalter in LTSpice.
Die gezeigte Methode hier ist nur einfache Mathematik, in der Messtechnik und Schaltungsentwicklung vorteilhaft und oft zu gebrauchen.
Tau=100µF*22k
Tau=100*10^-6 *(As/V) * 22000*(V/A) ==> die Einheiten lassen sich kürzen auf s = Sekunde
Tau=2,2 Sekunden
In der Cursorposition bei ca. 2,2s ist die Kondensator Spannung auf ca. 36,8% abgesunken, was dem Wertepaar für Tau entspricht.
Man vernachlässige bitte die wenigen Millisekunden Verzögerung in der Simulation durch das Aufladen von C1. Diese Simulation ist zugleich ein schönes Beispiel hierfür, wie man in LTSpice die Schalter editieren muss, auch zum späteren Nachschlagen geeignet, denn ich vergesse auch ständig immer wieder die Syntax zum Einstellen der Schalter in LTSpice.
- Ron=Durchlasswiderstand Schalter
- Roff=Sperrwiderstand Schalter
- Vt=Triggerspannung ab welcher der Wechsel zwischen Ron und Roff stattfindet
- Vh=Hystere der Triggerspannung (genaue Funktion bitte in der LTSpice Hilfe nachlesen)
Die gezeigte Methode hier ist nur einfache Mathematik, in der Messtechnik und Schaltungsentwicklung vorteilhaft und oft zu gebrauchen.